Double DQN Applied To Lunar Lander

Lunar Lander Environment

This project aims to train a Double Deep Q-Learning Network (Double DQN) agent to successfully land a Lunar Lander, run via the python library Box2D within Open-AI Gym.

This is a deterministic environment (the next state is solely determined by the action taken, no uncertainty) which provides a fully observable mixed observation space. Each observation of the environment’s state consists of coordinates relative to origin, velocity components and whether each leg is grounded. There four actions available to the lander – fire one of three thrusters or do nothing.

The environment is considered ’solved’ when the episode score reaches 200 points or more. Roughly 100-140 points are awarded for safely arriving on the landing pad, 10 points for each leg being in contract with the ground (i.e. landing upright) and an additional ±100 points for a crash landing or arrival at rest respectively. To discourage long engine fires, the lander receives -0.3 points for each frame that the main/side engine is firing. This allows the agent to first learn how to stabilise its flight and then focus on perfecting the landing itself. With a random policy, as seen in the video below, the agent reaches a score of -180.

Prerequirements

The project is written in Python and, before starting, make sure to install and import the following libraries.

Double DQN Agent

Foundational Reinforcement Learning methods, such as Dynamic Programming, Monte Carlo and Temporal Difference Methods, rely on tabular constructs to train the agent to solve a particular environment. However, the environment at hand contains an observation space consisting of six continuous variables, of which five can range between positive and negative infinity, meaning a tabular Reinforcement Learning method would be ill-suited. The best method to overcome this is Deep Q-Learning which is the Deep Learning function approximator version of Q-Learning, a model-free tabular learning method. A Deep Q-Learning Network (DQN) is an algorithm constructed via combining fundamental Reinforcement Learning techniques with deep neural networks.

The main idea of Q-Learning is that each state-action-pair has a Q-value, the expected rewards for an action taken in a given state, based on which the optimal policy can be chosen. For DQNs, the Q-value cannot be determined exactly, but is approximated with a Deep Neural Network. Thus, the table is replaced with a Deep Neural Network that can handle continuous state input. Finding the best training algorithm for the Deep Neural Network, poses a great challenge. Consequently, multiple forms of DQN were proposed in recent years. Here, Double DQN was chosen, as it is relatively easy to understand and implement, but equally powerful.

Double DQN, as most other DQN algorithms, train the model using experience replay, a technique where the model is trained each timestep using a random subsample of recent experiences. Those experiences are sampled from a replay buffer that contains state, action, reward, and next state for a given number of the most recent timesteps.

Instead of using one Neural Network, Double DQN employs two different networks – the policy and the target network. The policy network, as the name implies, is responsible for choosing the optimal policy and is updated every timestep. The target network approximates the Q-value for the next state that is needed for the update equation. However, and here comes the crux of Double DQN, the optimal action of the next state is not chosen by the target network, but the policy network. By assigning different roles while performing the weight updates, overestimation of the Q-value for a chosen action is avoided, making the model generally more robust.

Below, you find the pseudocode for Double DQN, as well as the implementation in Python with comments.

Hyperparameters

You can find the hyperparameters that worked best for me, underneath. The action policy, especially in the beginning, is quite random, encouraging a lot of exploration.

Agent Training

Now that we have implemented the Double DQN agent, we can run the training process. As you can see in the convergence graph below, the model converges after roughly 400 episodes and is stable thereafter.

Model: "model_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_3 (InputLayer)         [(None, 8)]               0         
_________________________________________________________________
dense_6 (Dense)              (None, 128)               1152      
_________________________________________________________________
dense_7 (Dense)              (None, 128)               16512     
_________________________________________________________________
dense_8 (Dense)              (None, 4)                 516       
=================================================================
Total params: 18,180
Trainable params: 18,180
Non-trainable params: 0
_________________________________________________________________
Model: "model_3"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_4 (InputLayer)         [(None, 8)]               0         
_________________________________________________________________
dense_9 (Dense)              (None, 128)               1152      
_________________________________________________________________
dense_10 (Dense)             (None, 128)               16512     
_________________________________________________________________
dense_11 (Dense)             (None, 4)                 516       
=================================================================
Total params: 18,180
Trainable params: 18,180
Non-trainable params: 0
_________________________________________________________________
Episode 0 Reward -358.87 Average -358.87 Epsilon 0.99 Time 0.27 s
Episode 1 Reward -282.10 Average -282.10 Epsilon 0.99 Time 0.25 s
Episode 2 Reward -118.17 Average -227.46 Epsilon 0.99 Time 0.31 s

...

Episode 997 Reward 244.27 Average 249.01 Epsilon 0.1 Time 1.08 s
Episode 998 Reward 217.02 Average 248.45 Epsilon 0.1 Time 1.18 s
Episode 999 Reward 272.7 Average 248.39 Epsilon 0.1 Time 1.5 s

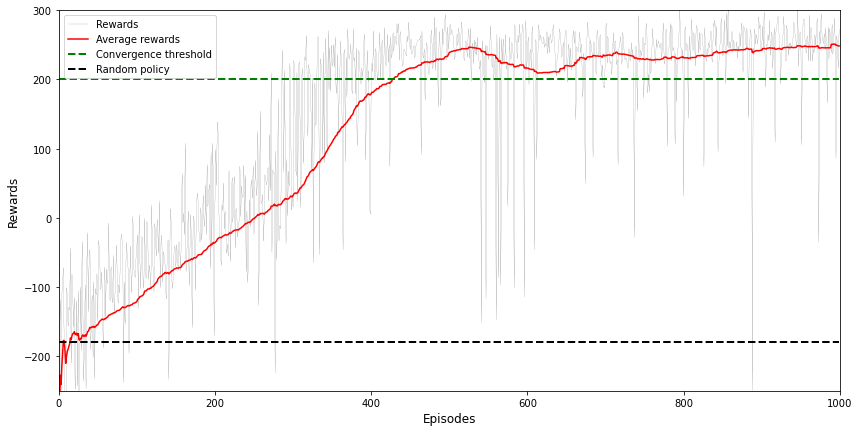
Below, you can see the agent’s policy improvement visualised over the whole training cycle.